Alternate Interior Angles are pairs of angles found on the interior of parallel lines but on the opposite side of the transversal.
In the figure below, parallel lines \(m\) and \(n\) are cut by the transversal \(t\).
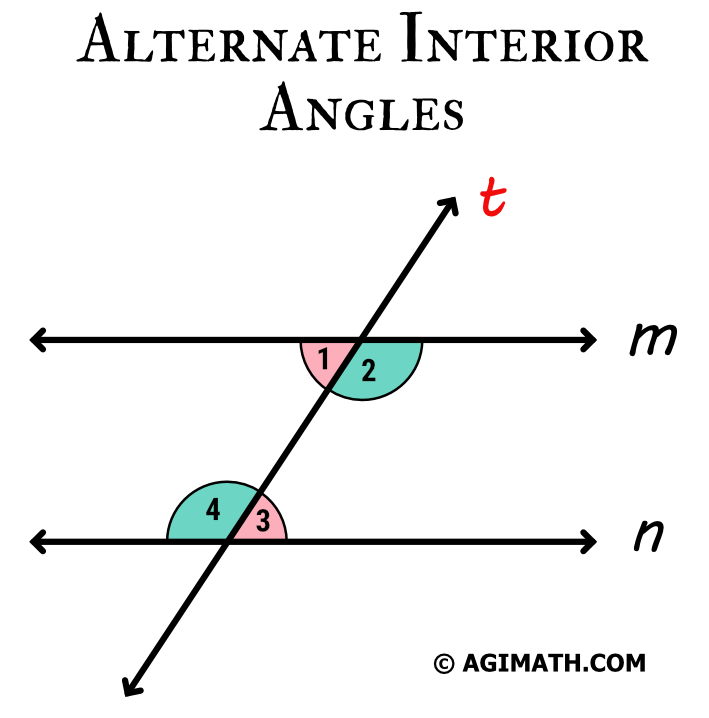
The pairs of the alternate interior angles are as follows:
\(\angle{1}\) and \(\angle{3}\)
\(\angle{2}\) and \(\angle{4}\)
Since the transversal intersected parallel lines, the alternate interior angles are congruent.
