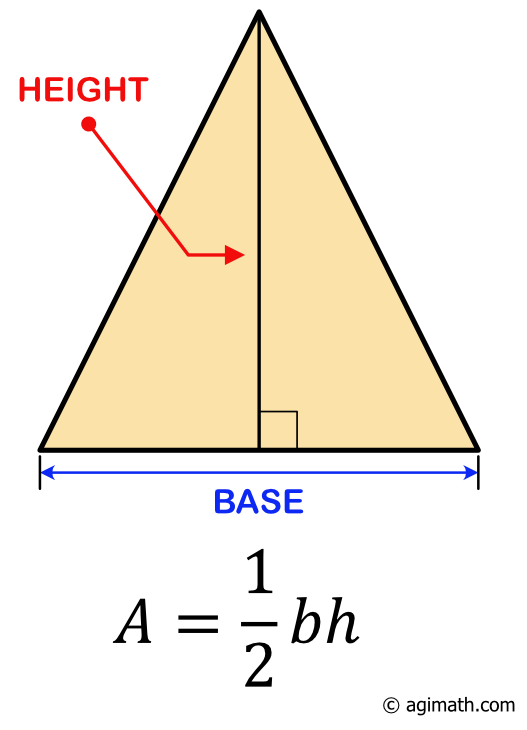
The area of a triangle is calculated by taking half \(\large{{1 \over 2}}\) of base \(b\) times height \(h\). The height here is perpendicular to the base which means they form a 90-degree angle at their intersection.
Example 1: A triangle has a height of \(12\) cm and a base of \(5\) cm. Find its area.
Since \(h=12\) and \(b=5\), we have
$$\eqalign{
A &= {1 \over 2}bh \cr
& = {1 \over 2}\left( {12} \right)\left( 5 \right) \cr
& = 30 \cr} $$
The area is \(30\) cm2.
Example 2: The area of a triangle is \(12.5\) km2. What is the height if the base is \(3\) km?
The given area is \(A=12.5\) while the base is \(b=3\). We plug in the values and then solve for the height, \(h\).
$$\eqalign{
12.5 &= {1 \over 2}bh \cr
12.5 &= {1 \over 2}\left( 3 \right)\left( h \right) \cr
12.5 &= {3 \over 2}h \cr
2\left( {12.5} \right) &= 3h \cr
{{2\left( {12.5} \right)} \over 3} &= h \cr
8.33 ≈ h \cr} $$
The base is about \(8.33\) km.
