The distance around a circle is called the circumference. It is similar to the perimeter of a rectangle which is the sum of all its sides. Though the word perimeter is usually reserved for polygons, shapes with straight edges.
To calculate the circumference of a circle, we only need to know its radius. The formula of the circumference is given by \(C = 2\pi r\) where \(r=\) radius and pi (\(\pi\)) has a numerical value that is approximately equal to \(3.1416\).
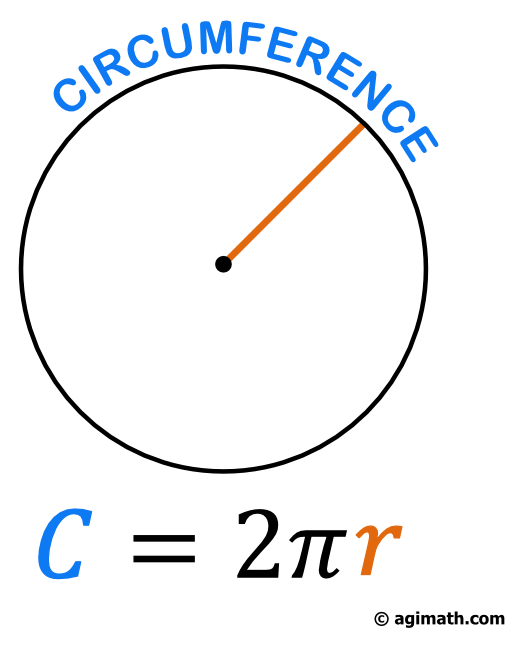
Example 1: What is the circumference of a circle with a radius \(6\)?
Since the radius of the circle is given, we just need to direct substitute that into the formula to get the measure of circumference.
$$\eqalign{
C &= 2\pi r \cr
& = 2\left( \pi \right)\left( \color{red}{6} \right) \cr
& = 12\pi \cr} $$
Therefore, the exact value for the circumference of the circle is \(12\pi\). Notice that we express our answer in terms of \(\pi\) if we want to give the exact answer.
However, if we want our answer as an approximation that means we will have to use also a numerical value for \(\pi\) which in this case is \(3.1416\).
$$\eqalign{
C &= 2\pi r \cr
& = 2\left( {3.1416} \right)\left( 6 \right) \cr
& = 37.6992 \cr} $$
The circumference is about \(37.7\), rounded to the nearest tenth.
Example 2: Find the circumference of a circle with a diameter \(5\)? Round your answer to the nearest hundredth. Use \(\pi=3.1416\).
Our first step is to determine the radius. Our diameter is given, so we can get the radius by dividing it by \(2\).
$$\eqalign{
r &= {1 \over 2}d \cr
& = {1 \over 2}\left( 5 \right) \cr
& = 2.5 \cr} $$
Now that we have the radius, we can calculate the circumference of the circle.
$$\eqalign{
C &= 2\pi r \cr
& = 2\left( {3.1416} \right)\left( \color{red}{2.5} \right) \cr
& = 15.708 \cr} $$
Therefore, the circumference is about \(15.71\) units.
