Corresponding Angles are pairs of angles that found on the same side of the transversal and located at relative positions of the intersection.
In the figure below, parallel lines \(m\) and \(n\) are cut by the transversal \(t\).
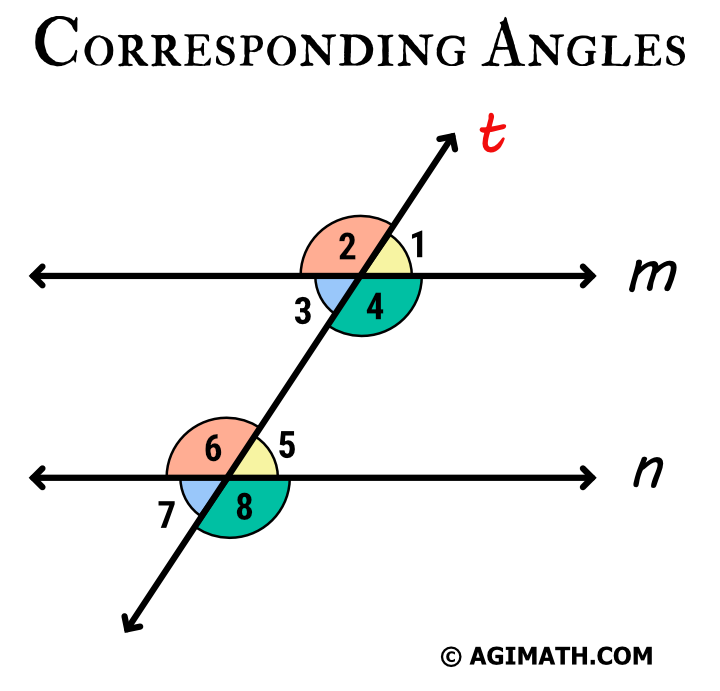
The four (4) pairs of the corresponding angles:
\(\angle{1}\) and \(\angle{5}\)
\(\angle{2}\) and \(\angle{6}\)
\(\angle{3}\) and \(\angle{7}\)
\(\angle{4}\) and \(\angle{8}\)
Since the transversal intersected parallel lines, the corresponding angles are congruent.
