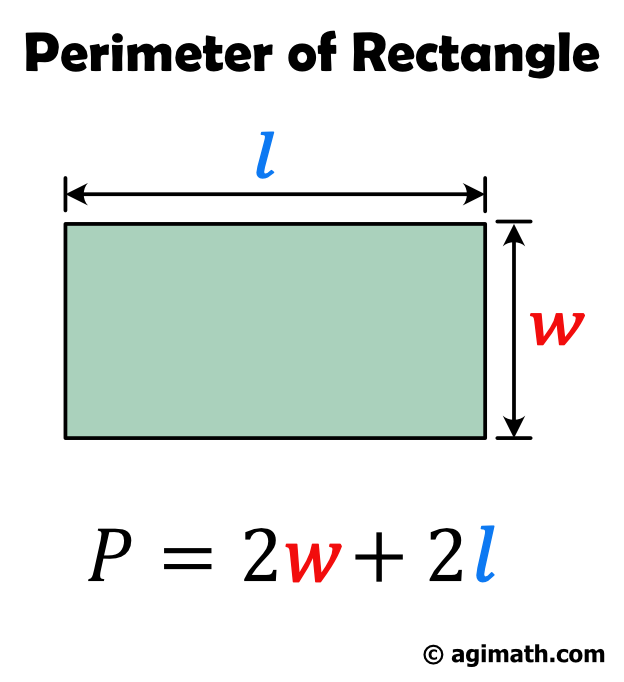
A rectangle is a geometric shape with two pairs of congruent sides. The shorter side is called the width while the longer side is called the width. If you know the width and the length of the rectangle, you should be able to find its perimeter. If the length of the rectangle is \(l\) and its width is \(w\), the perimeter is just the sum of all sides. That means, \(P=w+w+l+l\) which can be simplified as \(P=2w+2l\).
Example 1: A rectangle has a width of \(4\) feet and a length of \(7\) feet. What is its perimeter?
The width of \(4\) means we have \(w=4\). The length being \(7\) means that \(l=7\). A rectangle's perimeter is calculated using the formula \(P=2w+2l\). By substituting the known values and simplifying, we get
$$\eqalign{
P &= 2w + 2l \cr
& = 2\left( 4 \right) + 2\left( 7 \right) \cr
& = 8 + 14 \cr
& = 22 \cr} $$
Therefore, the perimeter is \(22\) feet.
Example 2: The perimeter of a rectangle is \(30\) inches. What is the length if the width is \(6\) inches?
The value of the perimeter is given which is \(30\). In addition, the width of the square is \(6\). That means we have \(P=30\) and \(w=6\). Let's substitute these values into the formula of the perimeter then solve for the length \(l\).
$$\eqalign{
P &= 2w + 2l \cr
30 &= 2\left( 6 \right) + 2l \cr
30 &= 12 + 2l \cr
30 - 12 &= 2l \cr
18 &= 2l \cr
{{18} \over 2} &= {{2l} \over 2} \cr
9 &= l \cr} $$
Therefore, the length of the rectangle is \(9\) feet.
